Les Lights: introductionL'éclairage, comme dans le monde réel, ainsi que dans le cinéma (je fais souvent cette analogie à ce milieu...), tient une place capitale dans le rendu des divers mondes en 3D que nous
allons créer. Comme dans la plupart des domaines en informatique, nous allons arriver à nos fins à coups de calcul mathématiques, et ce pour le plus grand plaisir de nos yeux.
Nous allons donc intégrer une notion supplémentaire au sein de la géométrie de nos objet, concernant la définition de nos points et nos triangles, qui est la notion de 'normale' à une
face. Sans trop rentrer dans les détails pour le moment, le vecteur normal d'une face est en fait le vecteur représentant la perpendiculaire au plan formé par une face ou une surface
donnée. Deuxième notion liée au normal face, chacun de ces vecteurs doit être normalisé (longueur comprise entre 0.0 et 1.0).
Donnons-nous le temps de voir les différents types composante des lumières:
La lumière ambianteLa lumière ambiante correspond au modèle le plus simple. On considère qu'il existe une source lumineuse présente partout et qui éclaire de manière égale dans toutes les directions.
Ce modèle de lumière correspond au niveau minimum d'éclairage qui sera appliqué sur les objets. En terme physique cela correspond un peu au soleil réfléchi par tout
l'environnement qui donne une sorte de lumière présente partout.
On définie l'intensité de cette lumière sur une surface comme suit :
Ip = pa*Ia Cette intensité lumineuse est constante sur toute la surface. 'Ia' désigne l'intensité de la lumière, 'pa' est le coefficient de réflexion de la lumière ambiante par la surface (0 <= pa <= 1).
'Ip' correspond à l'intensité de la lumière résultant de la réflexion sur la surface.
Prenons un objet fait d'une matière unique. pa reste constant sur la totalité de l'objet. Dans ce cas, l'objet apparait d'une seule et même couleur. Ce modèle d'illumination ne met pas
en valeur le volume d'un objet comme vous pouvez le voir sur la figure qui suit.
 La réflexion diffuse
La réflexion diffuseOn prend maintenant comme hypothèse que la source de lumière est ponctuelle et qu'elle émet de manière constante dans toutes les directions de l'espace.
Dans le modèle de réflexion diffuse, l'intensité en un point d'une surface dépend de l'angle formé entre le rayon de lumière qui touche le point de la surface et la normale à la surface.
Plus l'angle formé entre le rayon de lumière et la normale au plan est faible, plus l'intensité lumineuse réfléchie visible par l'observateur est forte.
Le principe physique qui se cache derrière ce modèle est simple. Notre source lumineuse émet une certaine énergie au mètre carré. Suivant l'incidence des rayons lumineux, cette
énergie sera répartie sur une plus ou moins importante surface de l'objet. Si les rayons et la surface sont perpendiculaires, alors l'énergie lumineuse sera répartie sur la plus petite
surface possible et donc l'énergie par unité de surface sera maximale (voir figure).
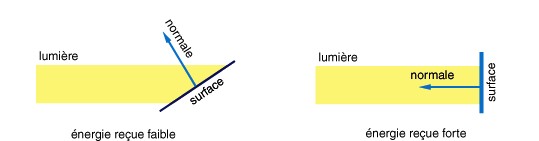
Maintenant, on sait pourquoi l'angle formé entre la normale au plan et les rayons de lumière est important. Par contre, on ne connait toujours pas la lumière qui sera réfléchie en
direction de l'observateur. Pour cela on se base sur les propriétés de la surface. Si on considère que la surface est une surface Lambertienne (surface mate) comme le papier ou la
neige, alors, on peut considérer que la lumière qui arrive sur la surface est réfléchie dans toutes les directions de manière égale. Dans ce cas, la position de l'observateur ne compte
pas. La lumière émise en direction de l'observateur dépend donc de l'intensité de la source lumineuse Il, de l'angle theta formé par le rayon de lumière et la normale au plan et du
coefficient de réflexion pd de la lumière diffuse par la surface (0 <= pd <= 1). On obtient la formule :
Ip = pd * Il * cos(theta)Pour la figure :
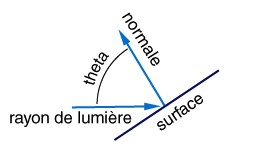
On notera au passage que si theta est supérieur à PI/2 alors c'est que la face n'est pas du tout éclairée par la source lumineuse car elle lui tourne le dos. Dans ce cas, l'intensité
lumineuse est 0.
Voici un exemple de réflexion diffuse :
 La réflexion spéculaire
La réflexion spéculaireLe modèle de réflexion spéculaire se différencie du modèle de diffusion en faisant intervenir le point d'observation. Dans ce modèle les rayons de lumière sont réfléchis par symétrie
par rapport à la normale à la surface. Ce modèle correspond aux propriétés de "miroir" des objets.
Il faut calculer quel est le rayon réfléchi sur la face. Ensuite, l'intensité de la lumière observée dépend de theta qui correspond à l'angle entre le rayon réfléchi et le point d'observation,
de l'intensité Il de la source de lumière et du coefficient de réflexion ps de la lumière spéculaire par la surface (0 <= ps <= 1). Si on se prend le rayon réfléchi dans l'oeil alors on a
l'intensité maximum. Autour de cela, on peut quand même voir quelque chose d'un peu atténué. Cela veut dire que la surface ne réfléchit pas directement la rayon mais qu'il y a une
certaine "diffusion" autour du rayon réfléchi. La fonction cosinus joue bien son rôle ici mais comme on veut pouvoir régler la diffusion autour du rayon réfléchi, on introduit le coefficient
n. On obtient la formule :
Is = ps * Il * cos(theta)^n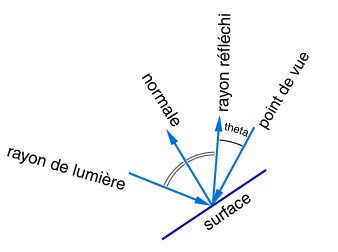
Voici un exemple de réflexion spéculaire :
 Atténuation de la lumière
Atténuation de la lumièreJusqu'à présent, on n'a pas pris en compte la distance entre la source lumineuse et la surface. On peut faire intervenir un coefficient d'atténuation de la lumière dans les modèles de
réflexion diffuse et de réflexion spéculaire pour pondérer l'intensité de la lumière en fonction de la distance.
Voici un exemple de coefficient de pondération :
fd = min(1/(c1+c2*dist+c3*dist^2), 1)On prend le minimum entre 1 et la valeur calculée pour que l'atténuation ne devienne pas une amplification.
Cette formule fait intervenir trois nouveau coefficients sur lesquels on peut jouer.
Pour utiliser cette formule dans les modèles de réflexion vus ci-dessus, il suffit de calculer la distance entre la source et le point pour lequel on calcul l'intensité de la lumière. Ensuite,
il faut calculer la lumière avec le modèle choisi ainsi que le coefficient fd. Le résultat de l'intensité correspond à la multiplication de l'intensité calculée par le coefficient de pondération
fd.
Modèle de lumière complexeMaintenant pour avoir des illuminations un peu complexes, on combine la lumière spéculaire avec la lumière diffuse et la lumière ambiante tout en faisant intervenir le coefficient de
pondération en fonction de la distance. Pour cela rien de plus facile, il suffit de calculer les intensités d'illumination pour chacun de ces modèles et de faire la somme des résultats pour
obtenir l'intensité de la lumière.
De la même manière, si on veut placer plusieurs sources de lumière dans une scène, il suffit de calculer l'intensité de la lumière sur une face pour chaque source et ensuite de faire la
somme de toutes les intensités pour avoir l'intensité résultat de l'ensemble des sources de lumière sur la face.
Utilisation de l'intensitéGénéralement, un point sur un écran (pixel) est représenté par 3 composantes : le rouge, le vert et le bleu. Si on considère la couleur marron. Elle peut se décomposer comme suit :
165 rouge, 42 vert, 42 bleu. Supposons que l'on ait calculé une intensité de 0.7 sur ce point marron. Si on veut obtenir le nouveau marron il suffit de multiplier les composantes rouge,
verte et bleue du marron pour obtenir le marron correspondant à l'intensité 0.7. On obtient alors : 115 rouge, 29 vert, 29 bleu.
Cela nous amène à une autre question. Les valeurs de rouge, de vert et de bleu sur un écran (dans une mémoire vidéo) sont bornées. Si on prend le cas où nos valeurs sont
comprises entre 0 et 255, on peut se demander ce qu'il se passe si on déborde. En effet, l'intensité de la lumière en un point peut être importante (8 par exemple). Dans ce cas, si les
valeurs débordent, on peut tout simplement se contenter de plafonner les valeurs à 255. Cela ne correspond pas à un modèle physique mais peut faire un peu comme un
éblouissement où tout devient blanc si la lumière est trop forte.
Voici un exemple qui met en oeuvre ce type de saturation en utilisant la lumière ambiante, la réflexion diffuse et spéculaire :
 Les modèles d'ombrage
Les modèles d'ombrageOn sait maintenant calculer l'intensité de la lumière en un point. Seulement pour des raisons de performance la plupart du temps, on ne calcule pas la lumière en chaque point. De
plus, la plupart des logiciels 3D modélisent les objets avec des polygônes. Seulement l'objet final souhaité n'est pas un objet avec un ensemble de faces plates. On ne peut pas mettre
une infinité de faces plates pour définir des objets courbes. Dans ce cas, il est quand même souhaitable d'avoir un aspect courbé.
Il existe plusieurs façons de procéder pour approximer la lumière en un point. On va voir les plus courantes.
L'ombrage plat On commence par la méthode la plus simple. On calcule la lumière pour un seul point de la surface que l'on veut représenter et on utilise la même intensité pour toute la surface.
Cette méthode à tendance a beaucoup faire ressortir les polygônes qui représentent un objet.
 L'ombrage de Gouraud
L'ombrage de GouraudLe principe de l'ombrage de Gouraud est de calculer l'intensité de la lumière pour les sommets du polygône et d'interpoler linéairement l'intensité des sommets pour déterminer
l'intensité en un point de la face. L'interpolation linéaire se fait sur le polygône projeté.
Cette technique permet d'avoir un lissage qui "gomme" les frontières entre les polygônes que l'on obtient avec un ombrage plat.
Voici un exemple de remplissage avec Gouraud :
 L'ombrage de Phong
L'ombrage de PhongL'ombrage de Phong est assez similaire à l'ombrage de Gouraud à la différence près que ce n'est pas l'intensité lumineuse des sommets que l'on interpole linéairement sur le
polygone 3D mais ce sont les normales des sommets.
En effet, si on revient un peu en arrière, on a vu que pour calculer l'intensité lumineuse en un point, on a besoin de la normale à la surface en ce point pour les modèles comme la
diffusion et la spécularitée. Avec l'ombrage de Phong, on interpole linéairement les normales des sommets pour déterminer une normale en chaque point et on se sert de cette
normale pour recalculer en chaque point l'intensité de la lumière. On se rend bien compte que cette méthode est bien plus coûteuse qu'un ombrage de Gouraud met elle permet un
meilleur rendu du modèle d'illumination spéculaire avec un plus petit nombre de polygône. En effet, la "tâche" de lumière peu être petite et même entièrement comprise dans un
polygône. Dans ce cas, si on calcule l'intensité aux sommets, elle ne sera pas importante alors qu'elle est importante au centre. Avec Gouraud, on ne la verra pas alors qu'avec Phong
elle apparaîtra car la lumière est recalculée en chaque point (même si c'est avec une normale interpolée).
La plupart des images qui illustrent les modèles de lumière ont été faites avec Phong. Mais voici un exemple révélateur du remplissage de Phong :
 Les différents type de lights
Les différents type de lightsLes lights sont des nodes comme les autres, et nous avons vu ci dessus, quelles étaient leurs influences sur les objets 3D. On peut, sur le plan informatique, les diviser en deux
grandes catégories:
1. Lumières Ambiantes:Petit rappel sur ce que l'on a vu : une lumière ambiante est une lumière tellement dispersée qu'elle n'a plus ni direction ni source. Une lumière ambiante illumine avec la même
intensité en tout point de la scène. Elle se définit par sa couleur et son intensité. Elle ne contribue à aucune réflexion spéculaire et est complètement indépendante des autres
lumières présentes dans la scène. Elle est la moins onéreuse (en termes de calculs) de tous les types de lumières.
2. Lumières directionnelles:Comme son nom l'indique, une lumière directionnelle possède une direction en plus d'une couleur et d'une intensité. La direction est la distance comprise entre le point d'origine
et la position courante de la lumière. On trouve trois sortes de lumières directionnelles, détaillées dans les
trois sous-chapitres qui suivent...PointUn point de lumière ne possède pas de direction et illumine de manière égale dans toutes les directions. Un feu de camp est un bon exemple de lumière point, une ampoule aussi.
Ces lumières sont plus onéreuses que les lumières directionnelles. A la différence de ces dernières, une lumière point possède une atténuation (l'intensité de la lumière décroît
avec la distance) et une distance d'éclairage (distante au-delà de laquelle la lumière n'illumine plus).
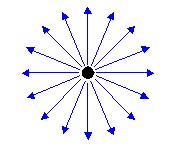 Directionelle
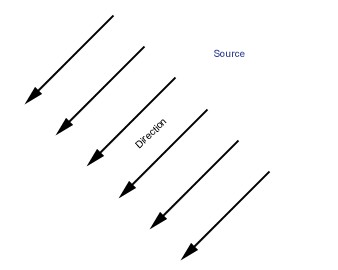
DirectionelleIl s'agit d'une source de lumière. Elle ne possède pas de position et produit une lumière qui parcourt la scène en droite ligne. Dans les jeux, elle est souvent utilisée pour reproduire
la lumière du soleil ou de la lune. Elle n'est pas très onéreuse mais à consommer toutefois avec modération pour éviter de faire pâlir votre fps.
 Spot
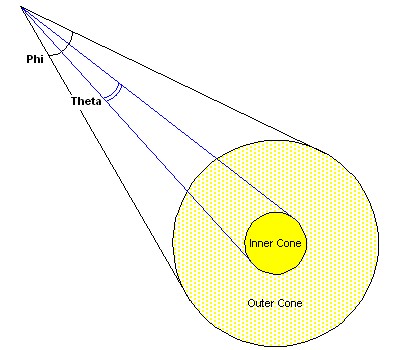
SpotUne lumière spot est comparable à celle d'une torche électrique ou des phares d'une automobile. Il s'agit de la lumière la plus compliquée à implémenter et la plus onéreuse en calcul.
Elle possède une direction et une position. L'intensité de la lumière est séparée en deux cônes. Dans le cône intérieur la lumière est plus intense que dans le cône extérieur. Seuls les
objets se trouvant dans un de ces cônes se trouvent illuminés. En plus de la position, direction, atténuation et distance d'éclairage, vous devez définir la taille des cônes et la façon
dont ils s'imbriquent.













![]()
![]()
![]()
![]()
![]()
![]()
![]() pour la reflexion diffuse tu dit que si l\'angle entre la source lumineuse et la normale est supérieur à pi/2, alors la face ne sera pas éclairé, mais si l\'angle fait pile poil pi/2, la face ne devrait pas être éclairé non plus ? enfin je suppose
pour la reflexion diffuse tu dit que si l\'angle entre la source lumineuse et la normale est supérieur à pi/2, alors la face ne sera pas éclairé, mais si l\'angle fait pile poil pi/2, la face ne devrait pas être éclairé non plus ? enfin je suppose ![]()
![]()
![]()
![]()